Chaos Game: Iterated Function System (IFS) 1
Im Kapitel Sierpinski n-Eck wurde zunächst
am Beispiel des Sierpinski Dreiecks ein simpler Algorithmus angegeben, mit dessen Hilfe man dieses Fraktal
erzeugen kann. Mit Hilfe dreier affine Abbildungen konnte man den Algorithmus realisieren.
realisieren. Welche affine Abbildung bei einem Rechenschritt angewandt wurde, war zufallsbestimmt.Verblüffend war
vor allem, dass man durch Zufall gesteuert ein determinstisches Shape erzeugt wurde.
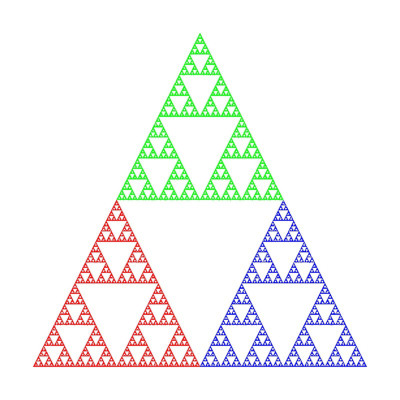
Die erwähnten drei affinen Abbildungen sind ein Beispiel für ein iteriertes Funktionensystem (IFS).
1981 erfand John Hutchinson diese Methode zur Fraktalkonstrukion . Barnsley machte sie in seinem Buch "Fractals Everywhere"
für ein größeres Publikum bekannt. Ein wesentlicher Aspekt behandelt die Nutzung von Selbstähnlichkeit,
um damit die IFSs damit zu erzeugen.
Wie funktioniert das beispielsweise für das Sierpinsky Dreieck?
Zweidimensionale affine Abbildungen kann man so darstellen:
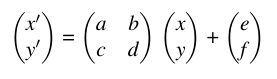
Wir legen zuächst fest, dass sich das große Dreieck in einem Einheitsquadrat im ersten Quadranten befindet.
Die erste Abbildung für das kleine rote Dreick erhält man aus dem großen Dreieck durch Verkleinerung mit Faktor 0.5,
also
a = 0.5, b = 0, c = 0, d = 0.5, e = 0, f = 0
Das blaue kleine Dreieck ist ebenfalls mit Faktor 1/2 verleinert und zusätzlich um 1/2 nach rechts verschoben. Somit gilt:
a = 0.5, b = 0, c = 0, d = 0.5, e = 0.5, f = 0
Das kleine grüne Dreieck wird mit 0.5 verkleinert und dann um 0.25 nach rechts und um 0.5 nach oben verschoben:
a = 0.5, b = 0, c = 0, d = 0.5, e = 0.25, f = 0.5
Der zugehörigen Sketch IFS2 kann am Ende der Seite heruntergeladen werden. Dort gibt es auch eine Version
IFS2A mit der man selbst Zufall spielen kann. Mit anderen Worten, man bestimmt jedes Mal, welche
affine Abbildung beim nächsten Iterationschritt verwendet werden soll. Dort erkennt man dann, dass die drei
Abbildungen genau den zuvor schon benutzen Algorithmus ergeben.
Nun aber zu einem Fraktal im Einheitsquadrat, für das wir noch keinen Algorithmus kennen:

Stellen Sie sich vor, Sie sollen zu linkem Fraktal das IFS finden. Die farbige Version daneben zeigt schon, wie
man vorgehen kann. Wir sehen fünf Teilfraktale, die entweder gleich oder ähnlich sind. Die unteren vier Fraktale
sind im Vergleich zum Gesamtfraktal um den Faktor 0.25 verkleinert. Rot: keine Verschiebung, grün: Verschiebung
in x-Richtung um 0.25 etc. Magenta: Verschiebung um 0.125 in x-Richtung und 0.25 in y-Richtung. Verkleinerungsfaktor
ist hier 0.75.
Das reicht bereits, um die fünf affinen Abbildungen zu formulieren:
a2=0.25; b2=0; c2= 0; d2=0.25; e2=0.25; f2=0;
a3=0.25; b3=0; c3= 0; d3=0.25; e3=0.5; f3=0;
a4=0.25; b4=0; c4= 0; d4=0.25; e4=0.75; f4=0;
a5=0.75; b5=0; c5= 0; d5=0.75; e5=0.125; f5=0.25;
if (z <= 100) {
V0(x, y, a1,b1,c1,d1,e1,f1);
stroke(255, 0, 0);
} else if (100 < z && z <= 200) {
V0(x, y,a2,b2,c2,d2,e2,f2);
stroke(0, 0, 255);
} else if (200 < z && z <= 300){
V0(x, y, a3,b3,c3,d3,e3,f3);
stroke(0, 255, 0);
} else if(300 < z && z <= 400){
V0(x, y, a4,b4,c4,d4,e4,f4);
stroke(255,0,255);
}else{
V0(x, y, a5,b5,c5,d5,e5,f5);
stroke(0,255,255);
}
 Von der Fläche her müsste man das türkise Sierpinsky Dreieck in dreiviertel aller Fälle wählen. Und die kleinen
Dreiecke jeweils in 1/16 -tel aller Fälle. Verändert man den Code oben entsprechend, dann bekommt man tatsächlich bei einer
ausreichenden Anzahl von Iterationen das Bild oben rechts.
Den ensprechenden Sketch IFS4 kann man am Ende der Seite herunterladen.
Um den Vorgang besser verstehen zu können, gibt es dort auch den Sketch IFS4A.
Nach dem Start sehen Sie das Fraktal in schwarz auf weißem Hintergrund. Durch die Tasten 1-5 wählen Sie die
nächste affine Abbildung. Die Taste R bewirkt einen Neustart. Sowohl vom Bild her, wie auch von der Rechnung,
sind 5 Fixpunkte zu sehen. Einmal die Ecken des Dreiecks und zusätzlich die Punkte (1/3;0) und (2/3;0). Wer mit
einer Maus arbeitet, kann einen beliebigen Punkt im Bild setzen. Dann wird von diesem Punkt aus die Iteration
weitergeführt.
Von der Fläche her müsste man das türkise Sierpinsky Dreieck in dreiviertel aller Fälle wählen. Und die kleinen
Dreiecke jeweils in 1/16 -tel aller Fälle. Verändert man den Code oben entsprechend, dann bekommt man tatsächlich bei einer
ausreichenden Anzahl von Iterationen das Bild oben rechts.
Den ensprechenden Sketch IFS4 kann man am Ende der Seite herunterladen.
Um den Vorgang besser verstehen zu können, gibt es dort auch den Sketch IFS4A.
Nach dem Start sehen Sie das Fraktal in schwarz auf weißem Hintergrund. Durch die Tasten 1-5 wählen Sie die
nächste affine Abbildung. Die Taste R bewirkt einen Neustart. Sowohl vom Bild her, wie auch von der Rechnung,
sind 5 Fixpunkte zu sehen. Einmal die Ecken des Dreiecks und zusätzlich die Punkte (1/3;0) und (2/3;0). Wer mit
einer Maus arbeitet, kann einen beliebigen Punkt im Bild setzen. Dann wird von diesem Punkt aus die Iteration
weitergeführt.

Affine Abbildungen können auch Drehungen enthalten. Diese Erkenntnis nutzen wir im nächsten Beispiel:

Durch die Farbwahl wird erkenntlich, dass hier ebenfalls in hohem Maß Selbstähnlichkeit herrscht. Es gibt vier Teile: roter Stiel, gelber Farn, blauer Farn und grüner Farn. Da die Objekte nicht nur verschoben und skaliert sind, müssen wir die Drehung hinzunehmen. So sieht die Abbildung in unserem Fall aus:
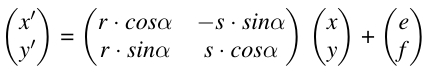
Um die vier affinen Abbildungen aufscheiben zu können, benötigt man den Winkel α, die Verschiebung e und f und die Skalierungsfaktoren r und s für x- bezw. y-Achse. Als Nullpunkt wird der untere Teil des Stiels festgelegt. Die Matrix Parameter sind dann:
a=r*cos α ; b= −s*sin α ; c= r*sin α; d=s*cos α
Der Stiel verläuft zu Beginn parallel zu y-Achse und wird später leicht gedreht und skaliert. Dass man genau den Faktor 0.16 wählt, ist keinesfalls zwingend. Entscheidend ist, dass bei der Erzeugung des Bildes die Proportionen stimmen.
Die Parameter r, s, α e und f sind nicht eindeutig. Auch andere, als die hier vorgeschlagenen Werte erzeugen ein Farn-ähnliches Bild. Die Winkel α kann man, sofern man einen echten Farn vor sich hat, messen.
Am Beispiel gelber Farnarm: r = −0.3; s = 0.37; α = −50° e = 0.125; f = 0.25;
Oben eingesetzt bekommt man a = −0.19 ; b = 0.28 ; c = 0.23 ; d = 0.24.
Weil wir noch einige Sketche, die IFSs verwenden, erstellen werden, lohnt es sich zwei Klassen einzuführen, und zwar class IFS und class IFSTransform. Die genaue Ausführung der Klassen kann man im Quelltext von IFSFarn am Ende der Seite nachlesen.
addTransform ist eine Methode der Klasse IFS und ist so implementiert:
transforms.add(new IFSTransform(a, b, c, d, e, f, prob, col, nr));
}
ifs1.addTransform(0, 0, 0, 0.16, 0, 0, wkt[1], color(255, 0, 0),1);
ifs1.addTransform(0.85, 0.04, -0.04, 0.85, 0, 1.6, wkt[2], color(0, 255, 0),2);
ifs1.addTransform(0.2, -0.26, 0.23, 0.22, 0, 1.6, wkt[3], color(0,0,255),3);
ifs1.addTransform(-0.19, 0.28, 0.23, 0.24, 0, 0.44, wkt[4], color(255, 255, 0),4);
Indem man eine affine Abbildung mit einer Farbe verknüpft, kann man kontrollieren, welche affine Abbildung für welchen Teil des Bildes verantwortlich ist. Will man ein möglichst realistisches Bild erzeugen, dann taugt diese Farbzuordnung nichts. Für diesen Zweck verwendet man besser eine Farbzuordnung, die wir bei Attraktoren schon mehrfach angewandt haben: die Trefferdichte-Methode. Wenn man viele Millionen Mal iteriert, dann werden die Pixel notwendigerweise mehrfach getroffen. Und die Anzahl der Treffer für ein bestimmtes Pixel bestimmt die Farbe des Pixels.
Wir lassen hierzu während der Iteration eine MatrixB = new int[cols][rows] mitlaufen, die lediglich die Treffer auf pixels[i + j*cols] zählt. Weiter benötigt man einen geeigneten Farbverlauf. Wenn die Anzahl der Treffer sehr stark variieren, sollte man die Logarithmus Funktion nutzen:
float farbWert = k*log(MatrixB[i][j]). Einen geeigneten Faktor k findet man durch probieren.

In diesem und in den folgenden Beispielen werden wir immer auch eine "Chaos-Variante" implementieren. Dieser Begriff soll anzeigen, dass einige Parameter zufällig gewählt werden, also zum Beispiel die Parameter b und c. Die restlichen bleiben wie sie sind. Hier ein Ergebnis:
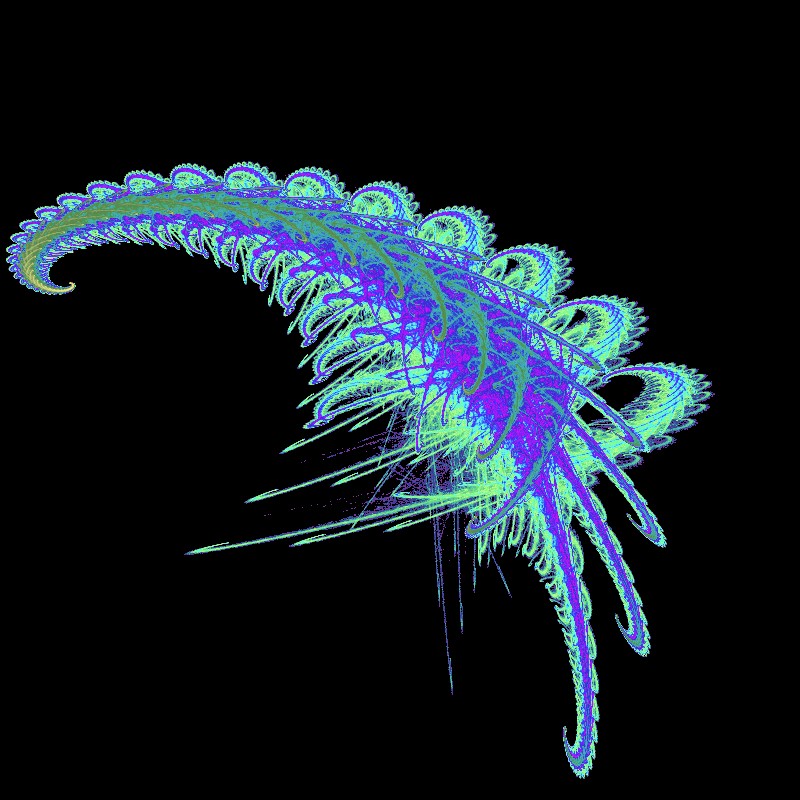
Wenn Sie den Prozess wie oben bei IFS4 in Zeitlupe beobachten wollen, dann laden Sie sich unten den Sketch IFSFarnA herunter. Dort können Sie mit Hilfe der Tasten e, h, t, G und R die Geschwindigkeit des Prozesses selbst bestimmen: e für einen Schritt, h für hundert Schritte und t für tausend Schritte auf einmal. Mit der Taste G wird die korrekte Gewichtung eingestellt und R startet das Programm von vorn.

Betrachtet man das einfarbige Bild eines Set Attraktor (siehe Bild links), so hat man keinerlei Information darüber, wie oft ein Pixel getroffen wurde. Treffer sind beispielsweise grün auf weißem Hintergrund. Auch das oben behandelte Sierpinsky-Dreieck gehört zu dieser Kategorie. Ein Set Attraktor ist eine Menge, die die Fixpunktgleichung erfüllt. Eventuelle Wahrscheinlichkeiten spielen hier keine Rolle.
Bei einem Measure Attraktor hingegen werden Wahrscheinlichkeitsmaße auf den Raum betrachtet. Die Information, wie oft ein Pixel getroffen wurde, kann als Maß dienen: in diesem Fall die Zuordnung Pixel -> Anzahl Treffer. Im einfachsten Fall nutzt man hierfür Transparenz. Häufige Treffer sind wenig oder gar nicht transparent. Anders ausgedrückt: Die Farbintensität macht den Unterschied zum obigen Set Attraktor.
Das so erzeugte Bild wirkt wesentlich realistischer als ein einfarbiges Bild eines Set-Attraktors. Als Measure-Operator verwendet man den Hutschinson-Operator.

Sketch IFS2 Sketch IFS2A Sketch IFS4 Sketch IFS4A
Sketch IFSFarn Sketch IFSFarnDichte Sketch IFSFarnA
Sketch measureAttractorFarn
Menu