Menu

Chaos Game: Sierpinski n-Ecke

Weshalb es funktioniert

Wie kann aus einer zufälligen Verteilung der Punkte das Sierpinski-Dreieck entstehen? Hexerei? Schauen Sie sich folgendes Bild an: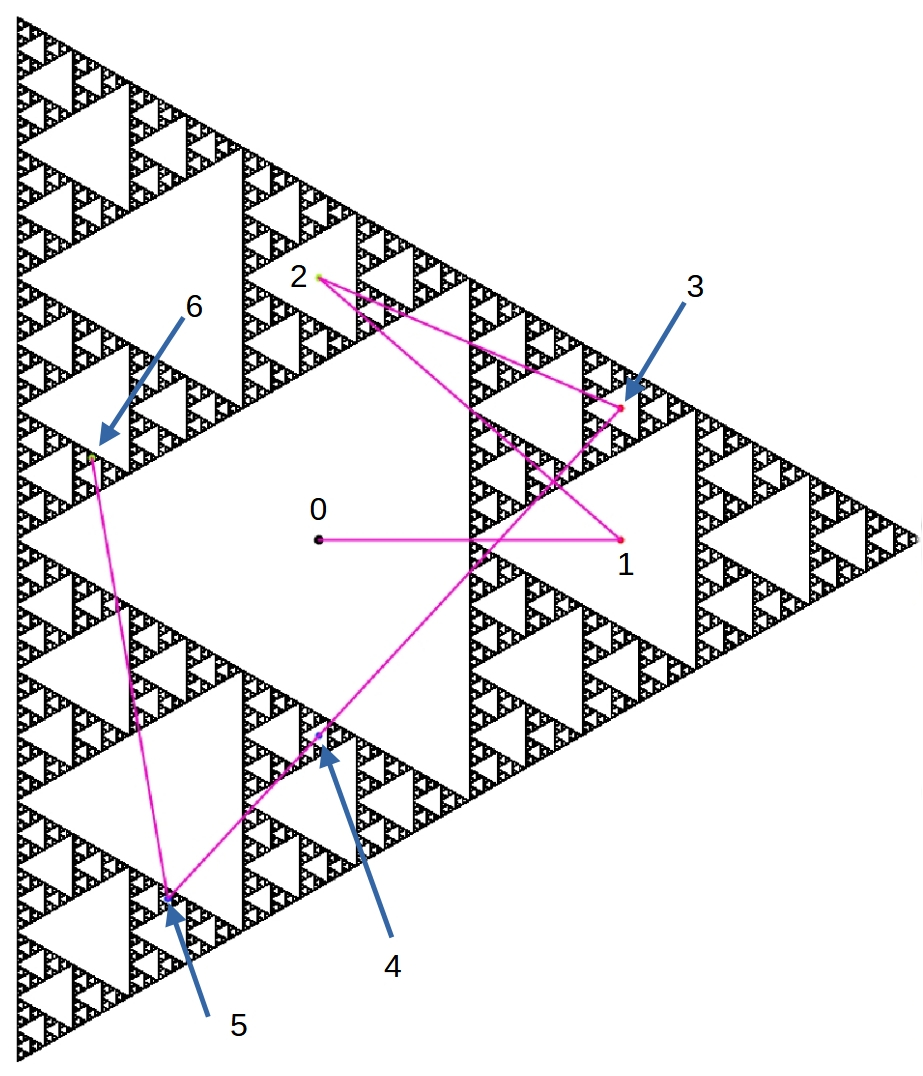

Einige 100000 Punkte (in schwarz) wurden, dem Alogrithmus entspechend, bereits eingetragen. Nun verfolgen wir einen Startpunkt im großen Innendreieck auf seinem weiteren (zufälligen) Weg. Es fällt auf, dass alle sechs nachfolgenden Punkte in einem weißen immer kleiner werdenden Dreieck landen. Beim sechsten Iterationsschritt kann man das Dreieck gerade noch erkennen. Ginge man einige Schritte weiter, so wäre das getroffene Dreick nicht mehr sichtbar. Der Punkt würde auf einem schwarzen Punkt des Sierpinski-Dreiecks landen und diesen entsprechend einfärben. Das bedeutet zweierlei: Erstens sollte man die ersten 10 Elemente nicht einzeichnen und zweitens werden danach Punkte nur noch auf dem schwarzen Bereich landen. Zumindest sieht es in dieser Auflösung so aus. Könnte man unendlich tief in das Dreieck zoomen, so blieben nur unendlich viele Eckpunkte aller Dreiecke übrig, - Punkte ohne Ausdehnung. Von daher besitzt das Sierpinski Dreieck die Fläche 0. Seine fraktale Dimension beträgt 1,585.

Kissing-Ratio

Funktioniert das Chaos Game auch mit mehr als 3 Ecken? Schauen wir uns den Fall für fünf Ecken an. Die Eckpunkte eines regelmäßigen Fünfecks lassen sich ganz einfach erzeugen, wenn man Polarkoordinaten verwendet. Der erste Punkt wird auf die x-Achse gesetzt. Sein Abstand zum Ursprung sei R. Im folgenden bleibt der Radius unverändert. Man muss nun lediglich 360 Grad durch 5 teilen, um den Winkel zum nächsten Punkt zu erhalten. So erhält man letztendlich alle Eckpunkte. (n ...Anzahl der Eckpunkte, w = 2· π/n)

Verwenden wir zunächst wie beim Dreieck den Faktor 0.5. Dann bekommen wir folgendes Bild:

Enttäuschend, oder? Die Teile überlagern sich. Und damit ist dies kein Sierpinski Fünf-Eck! Was bei drei Ecken funktioniert hat, klappt mit fünf Ecken nicht mehr. Die Frage ist offensichtlich: Welchen Faktor muss man bei n Ecken wählen, damit die einzelnen Teile sich gerade berühren? Diesen von n abhängigen Faktor nennt man Kissing Ratio (kR). Für n = 5 findet man, dass kR etwa 0.62 sein muss. Für n = 6 erhält man als Kissing Ratio, ebenfalls durch probieren, etwa 0.67. Wählt man diese kR-Werte, dann sehen die beiden Sierpinski n-Ecke so aus:


Um sich das mühevolle Herantasten an kR zu ersparen, benötigt man eine Formel, die den Wert in Abhängigkeit von n angibt.
Mit Hilfe der folgenden Skizze (Idee Tom Bates) kann man die gesuchte Formel herleiten. Zu sehen ist ein kleiner Ausschnitt eines regelmäßigen Neunecks (blaue Linien). Nun sollen die "Kind-Neunecke" innen so eingepasst werden, dass eine bzw. zwei Seite der kleinen Neunecke auf einer Seite des großen Neunecks liegen. Wenn wir kR bestimmen wollen, müssen sich die kleinen Neunecke zusätzlich berühren. Diese Berührung findet für n = 9 am dritten Eckpunkt des kleinen Neunecks statt (von der gemeinsamen Ecke 0 aus gezählt .
Für den Fall n = 9 gilt β = 2.5⋅2⋅α. Für allgemeines n ist der Faktor vor 2⋅α     ceil(n/4 - 0.5).
(Die Methode ceil() verwandelt ein float Attribut in integer. Und zwar so, dass die nächst höhere ganze Zahl gewählt wird. Beispiel: ceil(0.25) = 1)


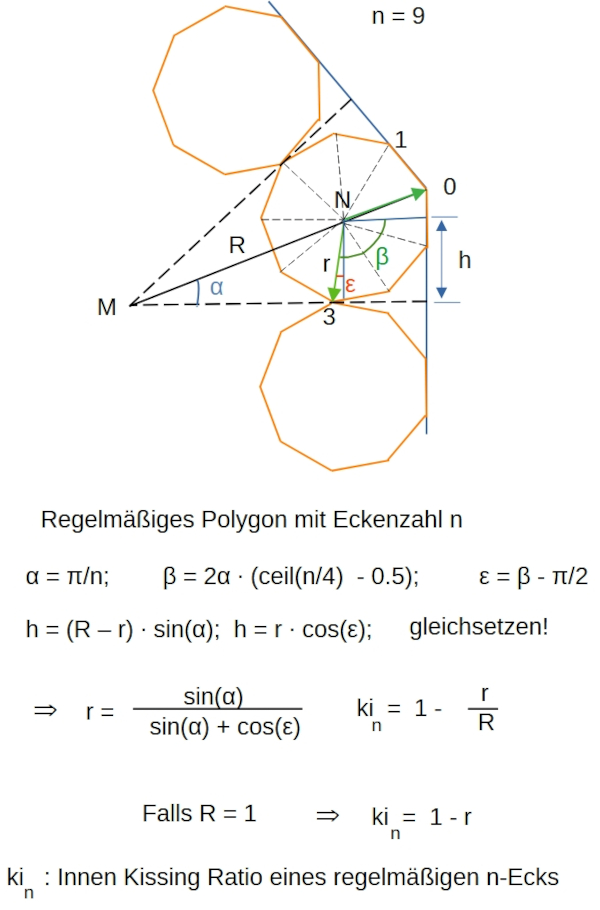
Nun könnte man die "Kind-Neunecke" auch außerhalb des großen Neunecks anbringen.
Hier gilt (ohne Beweis):    ka_n = 1 + r   wobei   ka_n : Außen Kissing Ratio eines regelmäßigen n-Ecks.
Die Kissing Rations ki und ka lassen sich in einer Methode bestimmen:
Für den Fall n = 5 liefert uns die Methode ki = 0.618034 und ka = 1.381966. Im Fall n = 6 sind es die Werte ki = 0.66666666 und ka = 1.3333333.
Die zusätzliche Verwendung von ka erweitert die fraktalen Sierpinski n-Ecke. Bleiben wir bei n = 5 und n = 6. Dann bekommt man mit der Erweiterung ka diese Bilder:

History

Schauen wir uns noch einmal das Sierpinski Dreieck an (Bild unten links). Die Selbstähnlichkeit steht außer Zweifel. Die Farbe allerdings macht nicht mit. Die Farbe kam dadurch zustande, dass man jedem Eckpunkt eine Farbe zugeordnet hatte und dann jedem eingezeichneten Punkt die Farbe der Ecke gab, die als letzte für die Iteration verwendet wurde. Zoomt man beispielsweise in das blaue "Kind-Dreick", so bleibt die Farbe immer genau gleich. Um das zu ändern, verwenden wir die Information, welche Ecke bei der vorherigen Iteration benutzt wurde. Die Dreiecks-Punkte, auf die der schmale weiße Pfeil zeigt, müssen ein Schritt zuvor im lila Dreieck, auf die der breite weiße Pfeil zeigt, gewesen sein. Wir geben daher dem "Enkel-Dreieck" diese Farbe (Bild unten Mitte), dann ist zumindest in dieser Zoomstufe die Selbstähnlichkeit auch in der Farbe korrekt. Dazu muss man nur alle in der Iteration vorkommenden Ecken zum Beispiel in int[] history speichern. Die "history-Tiefe" beträgt in diesem Fall t = 1. Geht man noch einen Schritt weiter und verwendet man t = 2, dann bekommt man das Dreieck im Bild unten rechts. Eine history-Tiefe von mehr als t = 5 macht keinen Sinn, da von den "Ururenkel-Dreiecke" nur noch Punkte zu sehen sind.


So kann man die Idee in Processing realisieren:
Am besten, Sie testen all diese Möglichkeiten selbst in folgendem Sketch:

Tasten- oder Mausaktion	Wirkung
Taste n	Anzahl der Punkte verdoppeln
Taste +	Anzahl der Ecken um 1 erhöhen
Taste -	Anzahl der Ecken um 1 verringern
Taste h	ki und ka um 0.05 erhöhen
Taste t	ki und ka um 0.05 verringern
Taste a	Farben verändern
Taste 0	History-Tiefe 0
Taste 1	History-Tiefe 1
Taste 2	History-Tiefe 2
Taste 3	History-Tiefe 3
Taste w	Hintergrund weiß/schwarz
Taste k	Außenelemente zeichnen
Maus-Klick ins Fenster	Zoomen an dieser Stelle

Solange die Tasten "h" und "t" nicht gedrückt wurden, werden immer die Kissing Ratio ki und ka verwendet.

Sketch ChaosGameSierpinskiNEcke

Menu