Simulation
Gravitation
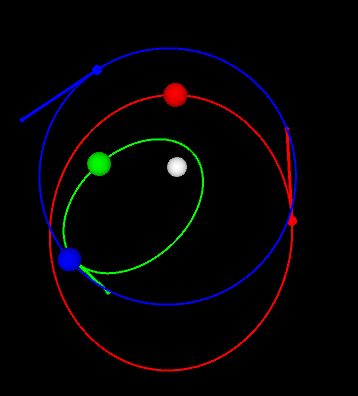
Mit dem hier vorgestellten Sketch "Gravitation" kann man Bewegungen mehrer Massen in einem Schwerefeld simulieren. Es wird
davon ausgegangen, dass der Zentralkörper (weiß) eine erheblich größere Masse hat, als die "Planete".
Daher vernachlässigen wir die Wirkung der Gravitationskräfte der Planten untereinander.
(Bei ähnlich großen Massen ist
das System nicht einmal bei nur insgesamt drei Körpern lösbar. Siehe:
Drei-Körper-Problem.)
Mit dem ersten Klick bestimmt man den Ort eines Planeten zu einem Zeitpunkt t0 . Mit einem zweiten Klick
legt man seine Geschwindigkeit fest:
Je größer der Abstand der beiden Punkte, desto größer die Geschwindigkeit. Gleichzeitig wird dadurch auch die
Richtung der Geschwindigkeit festgelegt. Die Anzahl der Körper wurde hier auf drei festgelegt.
Also muss man noch weitere zwei mal durch je zwei Klicks die Anfangsbedingungen der restlichen beiden Köper festlegen.
Im Bild links sind Anfangsbedingungen durch die drei Strecken noch erkennbar.
Ein letzter Klick startet das Programm.
Einen Neustart bekommt man durch Klick in die untere linke Ecke.
Dies sind die zu lösenden Differenzialgleichungen:
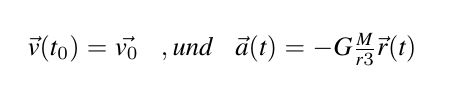
Um diese Differenzialgleichungen zu lösen ("Zweikörperproblem"), muss man eine Anfangsgeschwindigkeit für jeden Körper festlegen. lösen. Das Vefahren wurde schon beim Doppelpendel angesprochen. (Siehe: "Runge-Kutta 4" ). Im Folgenden der Quellcode für das Runge-Kutta-4 Verfahren. Die Klasse vierDContainer wurde eingeführt, um auf bequeme Weise vier Rückgabewerte zu ermöglichen. (Ein ListArrayListArray hätte es natürlich auch getan.) Reibung wird bei der Berechnung berücksichtigt.
r= Math.sqrt(X*X+Y*Y);R=r*r*r;
vRK[0][0] = Vx; aRK[0][0] = -M*G*X/R;
vRK[1][0] = Vy; aRK[1][0] = -M*G*Y/R;
r= Math.sqrt(Math.pow(X+0.5*vRK[0][0]*dt,2)+Math.pow(Y+0.5*vRK[1][0]*dt,2));R=r*r*r;
vRK[0][1] =vRK[0][0] + 0.5*aRK[0][0]*dt ; aRK[0][1] = -M*G/R*(X+ 0.5*vRK[0][0]*dt);
vRK[1][1] =vRK[1][0] + 0.5*aRK[1][0]*dt ; aRK[1][1] = -M*G/R*(Y+ 0.5*vRK[1][0]*dt);
r= Math.sqrt(Math.pow(X+0.5*vRK[0][1]*dt,2)+Math.pow(Y+0.5*vRK[1][1]*dt,2)); R=r*r*r;
vRK[0][2] =vRK[0][0] + 0.5*aRK[0][1]*dt ; aRK[0][2] = -M*G/R*(X+ 0.5*vRK[0][1]*dt);
vRK[1][2] =vRK[1][0] + 0.5*aRK[1][1]*dt ; aRK[1][2] = -M*G/R*(Y+ 0.5*vRK[1][1]*dt);
r= Math.sqrt(Math.pow(X+vRK[0][2]*dt,2)+Math.pow(Y+vRK[1][2]*dt,2)) ; R=r*r*r;
vRK[0][3] = vRK[0][0] + aRK[0][2]*dt ; aRK[0][3] = -M*G/R*(X+ vRK[0][2]*dt);
vRK[1][3] = vRK[1][0] + aRK[1][2]*dt ; aRK[1][3] = -M*G/R*(Y +vRK[1][2]*dt);
X = X + (vRK[0][0] + 2*vRK[0][1] + 2*vRK[0][2] + vRK[0][3])/6*dt;
Y = Y + (vRK[1][0] + 2*vRK[1][1] + 2*vRK[1][2] + vRK[1][3])/6*dt;
Vx = Vx + (aRK[0][0] + 2*aRK[0][1] + 2*aRK[0][2] + aRK[0][3])/6*dt;
Vy = Vy + (aRK[1][0] + 2*aRK[1][1] + 2*aRK[1][2] + aRK[1][3])/6*dt;
if(mitReibung){
float qV = sq((float)Vx)+sq((float)Vy);
Vx = Vx*(1-qV*0.000002); Vy = Vy*(1-qV*0.000002);
}
return new vierDContainer(X,Y, Vx, Vy);
}
Man kann im unteren Teil erkennen, dass der Prozess auch mit Reibung (proportional zum Quadrat des Geschwindigkeitsbetrages) laufen kann. Mit hilfe der r -Taste kann man beliebig oft zwischen "Reibung" und "ohne Reibung" umschalten. Probieren Sie es aus:
Ohne Reibung erhalten wir als Laufbahn, je nach Anfangsbedingungen, Ellipsen, Parabeln
und Hyperbeln gemäß den newtonschen Graviationsgesetzen. Schaltet man die Reibung ein, so sind die
Laufbahnen erwartungsgemäß nicht stabil:

Menu