ChaosGameVarianten

Chaos Game: Sierpinsky n-Eck Varianten

Überblick

Schauen wir uns zunächst an, was man im Vergleich zum letzten Kapitel anders machen kann. Es sind vier Dinge:

1. Man verwendet anstatt des Kissing-Ratios einen anderen Ratio-Wert.

2. Die Eckpunkte müssen kein regelmäßiges n-Eck bilden. Die Kissing-Ratio-Formel ist dann aber nicht mehr gültig!

3. Man ändert die Chaos-Game Regel.

4. Die bisher verwendete affine Abbildung, die sich aus der Iterationsvorschrift ergab, ist sehr speziell. Man kann sie durch eine beliebige affine Abbildung ersetzten.

5. Im Anschluss an die affine Abbildung kann eine nicht-affine Abbildung angewandt werden.

In diesem Kapitel kümmern wir uns um die Punkte 1 bis 3. Die Punkte 4 und 5 bekommen je ein extra Kapitel.

1. Fall: n = 4

Unter allen regelmäßigen n-Ecken sticht ein Fall heraus. Das Quadrat! Ein Sierpinski Quadrat gibt es offensichtlich nicht. Kissing Ration für n = 4 ist ki = 0.5. Und so wie unten links sieht das Ergebnis aus:

Auch wenn es hier so aussieht - einen Attraktor gibt es hier nicht! Die farblich unterschiedenen vier Teilquadrate, die die zur entsprechenden Ecke zugehörigen Punkte markieren, sind nicht "flächenfüllend". Im zweidimensionalen reelen (Teil-)Raum ist die Anzahl der Punkte überabzählbar unendlich, bei einer Iteration aber nur abzählbar unendlich . Von einem Fraktal kann also keine Rede sein. Erhöht man aber ki nur geringfügig, etwa ki = 0.55, dann sieht das Ergebnis (oben rechts) dem Cantor Dust ähnlich. Und der ist mit Sicherheit ein Fraktal. Im Folgenden lassen wir jedoch ki mit 0.5 unverändert und variieren lediglich die Chaos Game Regeln.

2. Fall: n = 4 und Chaos Game Regel mit erster Veränderung

Die erste Veränderung ist scheinbar gerinfügig. Wir verlangen, dass niemals zwei gleiche Ecken hintereinander gewählt werden dürfen. Im Array history[] sind alle gewählten Ecken gespeichert. Im Programm-Code muss lediglich folgender Einschub eingetragen werden:

while(history[i+t-1]==history[i+t] ){
j =round(random(0-0.5,n-0.5));
history[i+t] = j;
}

Eine scheinbar unwichtige Änderung in der Regel, und schon sieht das Ergebnis völlig anders aus. Im Bild oben links wurden nur die Punkte mit ki = 0.5 eingetragen (plus zoom), daneben zusätzlich mit ka = 1.5.

3. Fall: n = 4 und Chaos Game Regel mit zweiter Veränderung

Die zweite Veränderung schränkt weiter ein: Wurde eine Ecke zwei Mal hintereinander gewählt, darf die nächste Ecke werder die vorherige noch die nachfolgende Nummer besitzten. Ein Beispiel: Es wurde zwei Mal hintereinander Ecke 3 gewählt. Dann darf die folgende Ecke weder Ecke 2 noch Ecke 4 sein. Bei insgesamt vier Ecken kommen hier nur erneut die Ecke 3 oder Ecke 1 in Frage. Die Realisierung dieser Bedingung im Programmcode ist etwas trickreich:

while(history[i+t-1]==history[i+t-2] && ((abs(history[i+t]-history[i+t-1])==1 ||
(history[i+t-1]== n-1 && history[i+t]==0) || (history[i+t-1]== 0 && history[i+t]==n-1)))){
j =round(random(-0.5,n-0.5));
history[i+t] = j;
}

Mit dieser zweiten Regeländerung erhalten wir ein komplett anderes Bild. Im Bild oben links wurden nur die Punkte mit ki = 0.5 eingetragen (plus Zoom), daneben zusätzlich mit ka = 1.5 (ohne Zoom).

4. Fall: n = 4 und Chaos Game Regel mit variabler Veränderung

Treiben wir das Spiel auf die Spitze! Und so gehen wir vor:

Bestimme einmalig ein natürliche Zahl g kleiner gleich 10. (Oberhalb g = 10 ändert sich das Ergebnis nicht wesentlich.)
Wähle bei jeder Anwendung der CG Regel eine natürliche Zahl tZ ungleich Null, aber kleiner gleich g.
Bestimme history[i+t-tZ], also diejenige Ecke, die tZ Schritte vorher gewählt wurde.
Dann darf die aktuelle Ecke history[i+t] nicht gleich der tZ Schritte zuvor gewählen Ecke history[i+t-tZ] sein.

Beispiel: Die aktuelle Ecke wäre 4. Die Zufallszahl tZ hätte 5 ergeben. Nun schlägt man nach, welche Ecke fünf Schritte zuvor gewählt wurde. Sagen wir es wäre die Ecke 4. Das heißt, man muss die aktuelle Ecke solange ändern, bis nicht mehr 4 gewählt wird. Und dies machen wir bei jedem Punkt innerhalb der Iteration. Das muss doch Chaos geben, oder?

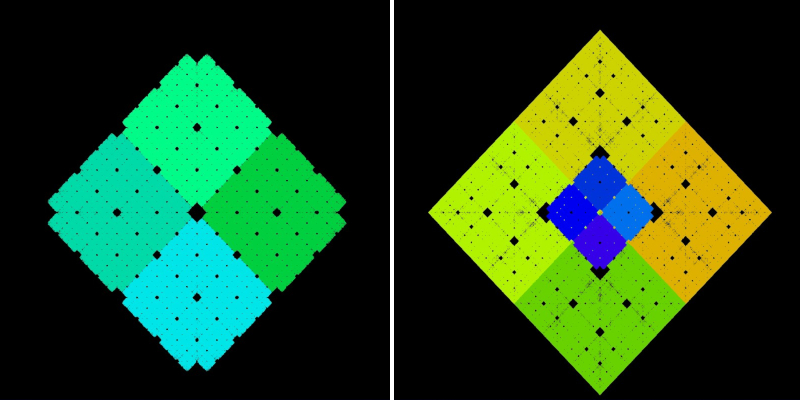
Offensichtlich nicht! Im Bild oben links wurden nur die Punkte mit ki = 0.5 eingetragen (plus zoom), daneben zusätzlich mit ka = 1.5. So realisieren wir diese neue CG Regel:

tZ =round(random(0.5,g-0.5));
while(history[i+t-tZ]==history[i+t] ){
j =round(random(0-0.5,n-0.5));
history[i+t] = j;
}

Für das obige Bild wurde g = 4 gewählt. Das heißt, tZ nimmt in unregelmäßiger Reihenfolde die Werte 1,2 und 3 an. Für g = 2 bekommen wir den 2.Fall. Je größer g, desto ähnlicher ist das Ergebnis dem 1.Fall.

5. Fall: n = 5 und Chaos Game Regel mit erster Veränderung

Wie im 2. Fall wird gefordert, dass niemals zwei gleiche Ecken hintereinander gewählt werden dürfen. Im Array history[] sind alle gewählten Ecken gespeichert. Im Programm-Code ist wie dort:

while(history[i+t-1]==history[i+t] ){
j =round(random(0-0.5,n-0.5));
history[i+t] = j;
}

Wie in den bisherigen Fällen werden die Ratios 0.5 und 1.5 verwendet. Diese sind für n = 5 keine Kissing-Ratios.

6. Fall: n = 8 und Punkte bilden kein regelmäßiges 8-Eck

Für das Bild unten wurden acht "Eckpunkte" gewählt: Die vier Eckpunkte des Quadrats und die vier Seitenhalbierenden der Seiten des Quadrats. Kisssing Ratio ist 0.66666666(Bild links). Der Wert für ki kann hier nicht aus der Formel bestimmt werden, da kein regelmäßiges n-Eck vorliegt. Entweder man findet den Wert für ki durch probieren oder man schaut sich das Bild etwas genauer an ;-)
Das entstehende Bild nennt man Sierpinski Carpet. Rechts daneben gilt Ratio = 0.7166 und history-Tiefe 1.

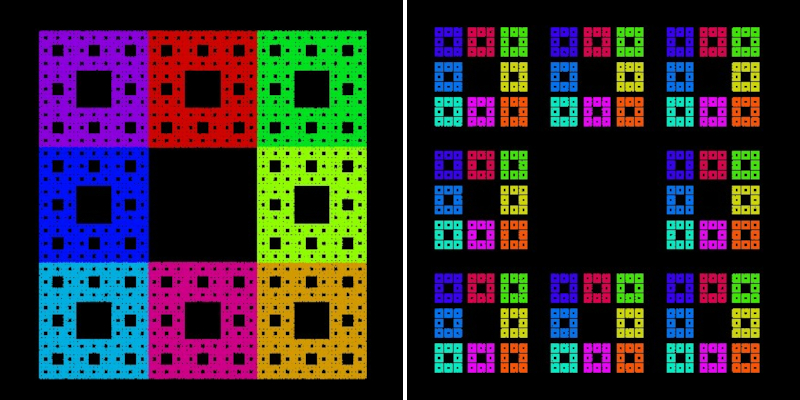
Die acht "Eckpunkte" des Carpets kann man kann man so bestimmen:

int id = -1;
for (int i = -3; i < 4; i=i+3) {
for (int j = -3; j < 4; j=j+3) {
if (i == 0 && j == 0) continue; // Mitte auslassen
id++;
.......(Parameter berechnen)..................
}
}

7. Fall: Beliebige Punkte

Damit man nachvollziehen kann, wie die Punkte in der Ebene das Ergebnis beeinflussen, verteilen wir die Punkte nicht allzu beliebig. In unserem Fall bilden sie einen Stern. Außerdem ist im Ursprung ein weiterer Punkt vorgegeben. Im Bild unten links handelt es sich um 17 Punkte. Es wurden zwei Ratios verwendet: 0.8 und 1.2. Zur besseren Erkennbarkeit verbinden wir alle Punkte außer dem Ursprung durch weiße Linien. Wie oben auch wird die Farbe durch die angestrebte Ecke bestimmt. 17 Ecken benötigen 17 Farben. Bei den Außenpunkten des Sterns erkennt man je Punkt zwei Farben, erzeugt durch zwei Ratios. In der Mitte ist die Sache etwas unübersichtlicher (Vergrößerung unten rechts). Zu sehen ist außerdem, dass wir hier zweifelsfrei einen Attraktor erzeugt haben.

Die Sternpunkte kann man recht einfach realisieren:

w = 2*PI/(n-1);
for(int i=0;i <n-1;i++){
Punkte[i] = new PVector();
if(i%2==0){
Punkte[i].x = vG*R*cos(i*w);
Punkte[i].y = vG*R*sin(i*w);
}else{
Punkte[i].x = vU*R*cos(i*w);
Punkte[i].y = vU*R*sin(i*w);
}
}
Punkte[n-1] = new PVector();
Punkte[n-1].x =0;Punkte[n-1].y=0;

Am besten, Sie testen all diese Möglichkeiten selbst in folgendem Sketch:

Tasten- oder Mausaktion	Wirkung
Taste x	Fall Nummer +1
Taste n	Anzahl der Punkte verdoppeln
Taste +	Anzahl der Ecken um 1 erhöhen
Taste -	Anzahl der Ecken um 1 verringern
Taste h	Ratio um 0.01 erhöhen
Taste t	Ratio um 0.01 verringern
Taste a	Farben verändern
Taste 0	History-Tiefe 0
Taste 1	History-Tiefe 1
Taste 2	History-Tiefe 2
Taste 3	History-Tiefe 3
Taste w	Hintergrund weiß/schwarz
Taste k	Außenelemente zeichnen
Taste i	Zoomen-in einmalig, zentral
Taste o	Zoomen-out einmalig, zentral
Maus-Klick ins Fenster	Zoomen an dieser Stelle

Sketch ChaosGame Sierpinski Varianten

Menu