3D mit Processing
Mandelbulb
Nach Entdeckung der
Mandelbrot-Menge in der komplexen Ebene
wurde lange geforscht, ob es möglich ist, derartige Fraktale auch in drei Dimensionen herzustellen.
Was man fand, waren anfangs lediglich die sogenannte
Quaternion Julia Fraktale , die
allerdings vierdimensional sind. Zur Darstellung in drei Dimensionen muss man "Schnitte" herstellen, die
jedoch eher einer Portion Spagetti ähneln, als einem Fraktal.
2009 schlugen D.White und P.Nylander schließlich vor, dreidimensionale Punkte im Raum durch ihre sphärischen
Koordinaten darzustellen und auf diesen die n-te Potenz auf folgende Weise zu definieren:
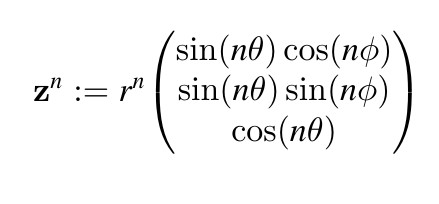
Ein Mandelbulb ist dann die Menge aller Punkte in ℝ3, für die die Folge
z → zn + c beschränkt ist. Der Vektor c durchläuft, wie bei der zweidimenionalen
Mandelbrot-Menge, alle Vektoren in dem zu untersuchenden Bereich. Konvergenz erwarten wir nur, wenn alle Werte
für x,y und z in einem Bereich zwischen -1 und 1 liegen. Erwähnt werden sollte auch noch, dass für den Exponenten
in der Regel n = 8 gewählt wird.
Voxelbild
Wie könnte man die Punkte im Raum, für die Konvergenz gilt, markieren?
Die Möglichkeiten sind: cube oder sphere, wobei ein
möglichst kleiner Wert für Länge bzw. Radius gewählt werden sollten: cube(1) oder sphere(1).
Man darf aber auch damit nur relativ grobe Bilder erwarten.
Wer das Kapitel Implizite Flächen durchgearbeitet hat,
kommt vermutlich auf die Idee,
gedanklich das gesamte Volumen in ein feines
Gitter zu stellen und dann Gitterpunkt für Gitterpunkt zu prüfen, ob dort Konvergenz vorliegt.
Genauer: Stellen Sie sich eine y-z-Ebene vor, die in einem genügend großen Abstand zum Mandelbulb, also
zum Beispiel bei x = -1.5 aufgestellt ist. Von dieser Ebene benötigen wir nur eine Fläche, die, falls
man nun in positive Richtung von x läuft, jeden Punkt des Mandelbulb erreichen kann.
Wenn Konvergenz einmal gefunden ist, dann setzt man dort ein cube ein
(sphere genötigt wesentlich mehr Rechenzeit) und geht dann zum nächsten Gitterpunkt, denn innere Konvergenzpunkte
sind glücklicherweise zur Darstellung des Körpers unnötig.
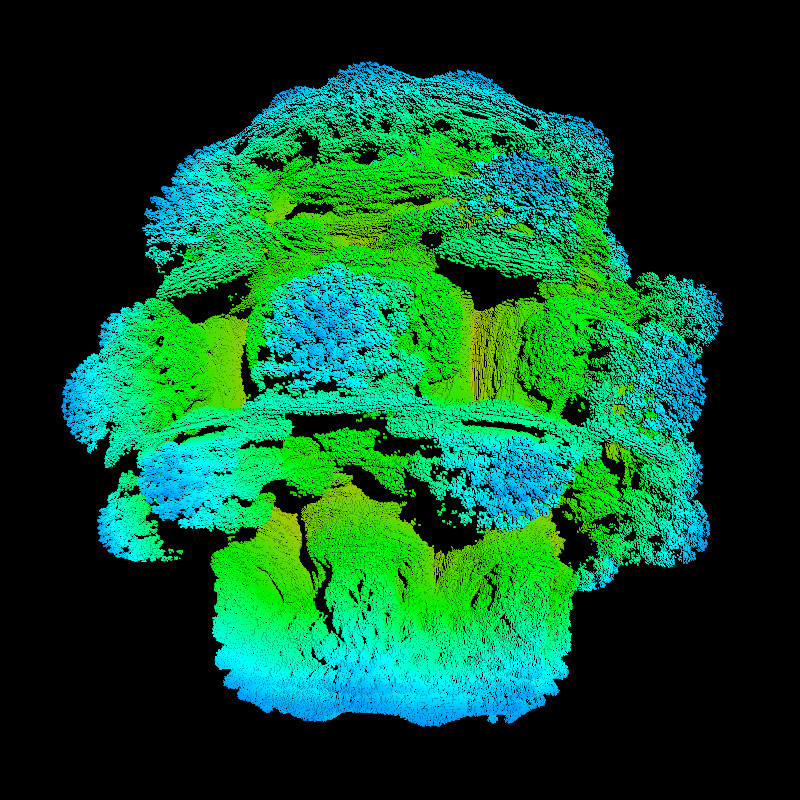
Das obige Bild besteht aus 400 000 Voxeln und benötigt, auch mit Multithreading, mindestens 2 Minuten Rechenzeit!
Die Fläche auf besagter y-z-Fläche hatte 800 x 800, also 640 000 Gitterpunkte, die alle durchlaufen werden
müssen. Weil wir von einem Würfelgitter ausgehen, gibt es 800 x 800 x 800 und somit 512 Millionen Voxel.
Von daher ist verständlich, dass man das Gitter in gleiche Abschnitte einteilen sollte. Die Anzahl wird durch
die Zahl der unabhängigen Cores des Prozessors bestimmt. Besitzt der Prozessor z.B. 8 Core, dann könnte man
die Fläche und damit das Gitter in 6 gleiche Teile zerlegen. Alle 8 Core zu verwenden, ist nicht ratsam,
da ja noch sehr viele andere Prozesse auf dem Rechner laufen.
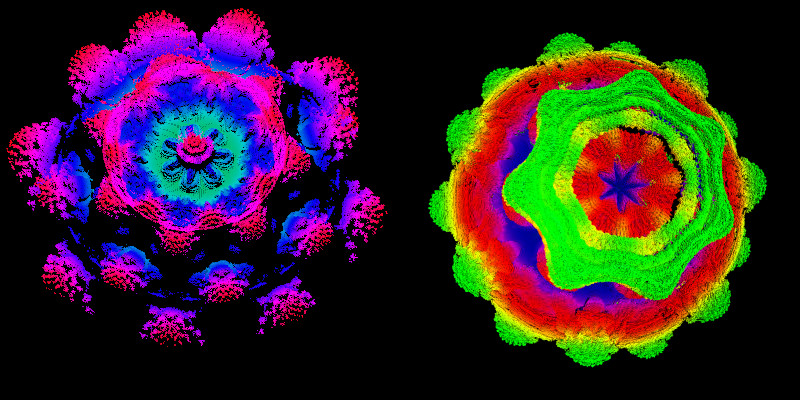
Ist ein Voxel nun bestimmt, an dessen Ort Konvergenz vorliegt, dann gibt es zwei Möglichkeiten, das
Voxel zu färben: Entweder durch den Abstand vom Ursprung oder durch den Abstand von der Fläche. Die
beiden Möglichkeiten lassen sich aber auch kombinieren.
Ebenso wie im Kapitel Implizite Flächen
arbeiten wir hier mit der PeasyCam. Das heißt, man kann das Bild mit der Maus bewegen und mit
dem Mausrad zoomen. Will man sich nun das Ergebnis von allen Seiten ansehen, ist man enttäuscht,
denn die, von der negativen x-Achse aus sichtbaren Voxel, liegen alle nur auf einer Seite!
Durch Koordinaten-Vertauschungen
kann man auch noch fünf weitere Richtungen hinzufügen. Allerdings sollte man dann das Gitter auf
400 x 400 x 400 Voxel beschränken. Selbst dann sind noch einige Lücken vorhanden, ebenso, wie
viele Voxel mehrfach, aus verschiedenen Perspektiven getroffen werden und somit den Sketch unnötig
verlangsamen.
Hier das "Herzstück" des Programm-Codes, die Überprüfung der Konvergenz:
int n = 8;
int iteration = 0;
while (true) {
Spherical c = spherical(zeta.x, zeta.y, zeta.z);
float newx = pow(c.r, n) * sin(c.theta*n) * cos(c.phi*n);
float newy = pow(c.r, n) * sin(c.theta*n) * sin(c.phi*n);
float newz = pow(c.r, n) * cos(c.theta*n);
zeta.x = newx + x;
zeta.y = newy + y;
zeta.z = newz + z;
iteration++;
b = c.r;
if (b > 2) {//Divergenz
break;
}
if(iteration > maxiterations) {
if (!treffer) {
treffer = true;
punktHinzu(I,(new MandelPoint(new PVector(x*200, y*200, z*200)))); // 'I' ist Nummer des Threads
} //end of if maxiteration
break;
} //end of if iteration
}//end of while
class MandelPoint {
PVector v;
MandelPoint(PVector v) {
this.v = v;
}
}
class Spherical {
float r, theta, phi;
Spherical(float r, float theta, float phi) {
this.r = r;
this.theta = theta;
this.phi = phi;
}
}
void punktHinzu(int n, MandelPoint p){
switch(n){
case 0: punkte00.add(p); break;
case 1: punkte01.add(p); break;
...........................
}
}
Mesh-Tracing
 Um das Verfahren des "Mesh-Tracings" zu verstehen, sehen Sie sich das Kapitel
Implizite Flächen an. Ganz am Ende des Kapitels
wird die "5. Idee" erklärt. Das hier verwendete Verfahren ist identisch - bis auf einen Punkt: Bei der
Bestimmung impliziter Flächen war ein "Treffer" gegeben, wenn die Einsetzung in die Gleichung kleiner als
ein gegebener Wert war. Hier ist ein Treffer vorhanden, wenn bei dem gegenen Punkt Konvergenz vorliegt.
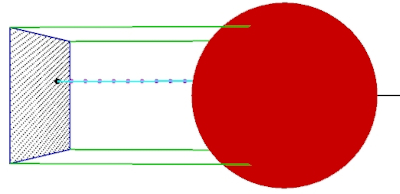
Die Projektionsfläche mit den Gitterpunkten im Bild links, kann man durch Drehungen
um die drei Achsen, mit Hilfe von Matrizen, in jede beliebige Position bringen. Der Abstand sollte so gewählt
werden, dass die Fläche außerhalb des abzubildenen Körpers liegt. Im Gegensatz zur vorherigen Methode, benötigt
man keinen 3D-Renderer. Die Färbung und Helligkeit der Pixel auf der Projektsionfläche wird durch den Abstand
des ersten Treffers zu Fläche und eventuell zum Ursprung bestimmt. Vorteil: Es gibt keine Lücken mehr.
Nachteil: Für jede neue Position muss die Rechnung erneut durchgeführt werden.
Um das Verfahren des "Mesh-Tracings" zu verstehen, sehen Sie sich das Kapitel
Implizite Flächen an. Ganz am Ende des Kapitels
wird die "5. Idee" erklärt. Das hier verwendete Verfahren ist identisch - bis auf einen Punkt: Bei der
Bestimmung impliziter Flächen war ein "Treffer" gegeben, wenn die Einsetzung in die Gleichung kleiner als
ein gegebener Wert war. Hier ist ein Treffer vorhanden, wenn bei dem gegenen Punkt Konvergenz vorliegt.
Die Projektionsfläche mit den Gitterpunkten im Bild links, kann man durch Drehungen
um die drei Achsen, mit Hilfe von Matrizen, in jede beliebige Position bringen. Der Abstand sollte so gewählt
werden, dass die Fläche außerhalb des abzubildenen Körpers liegt. Im Gegensatz zur vorherigen Methode, benötigt
man keinen 3D-Renderer. Die Färbung und Helligkeit der Pixel auf der Projektsionfläche wird durch den Abstand
des ersten Treffers zu Fläche und eventuell zum Ursprung bestimmt. Vorteil: Es gibt keine Lücken mehr.
Nachteil: Für jede neue Position muss die Rechnung erneut durchgeführt werden.
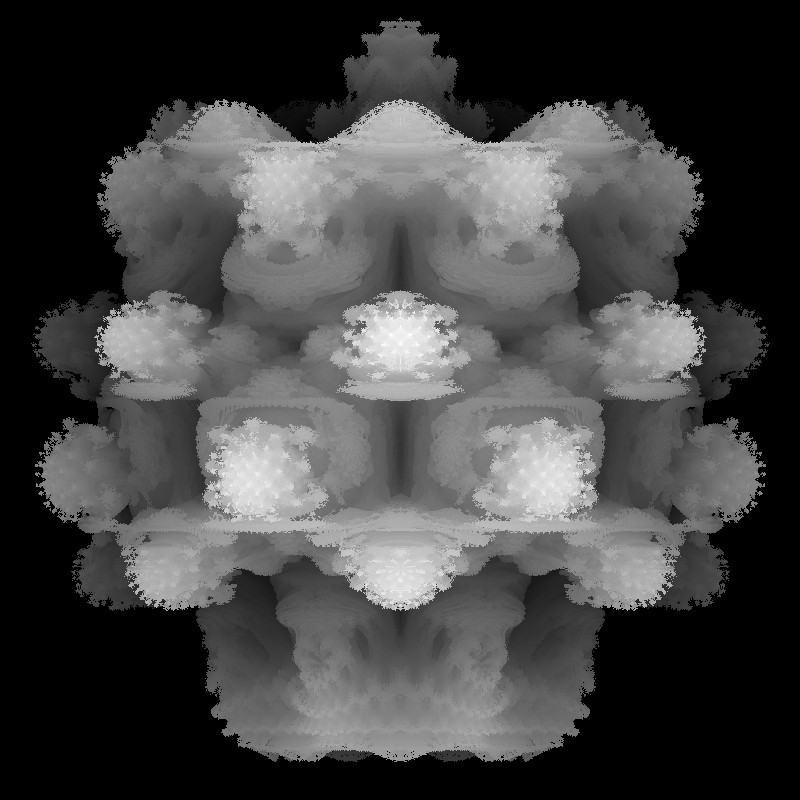
Das obige schwarz-weiß Bild bekommt man, Pixel für Pixel, indem man den "Grauwert" auf folgende Weise bestimmt:
Dabei ist abstand[n] der Abstand des Treffers vom Ursprung und n ist dabei die Nummer des Threads.
Mit Hilfe des Parameters k zählt man die Schritte von der Projektsionsfläche zum Treffer rückwärt:
Beginnend beispielsweise bei 255 und einem Treffer bei k = 100, bestimmt dieser Wert die Helligkeit des Pixels.
Nahe Treffer sind daher hell, ferne eher dunkel. Kein Treffer bedeutet, das zugehörige Pixel ist schwarz zu färben.
Farbe kommt ins Spiel, wenn man beispielsweise den Abstand des Treffers vom Ursprung farblich kodiert:
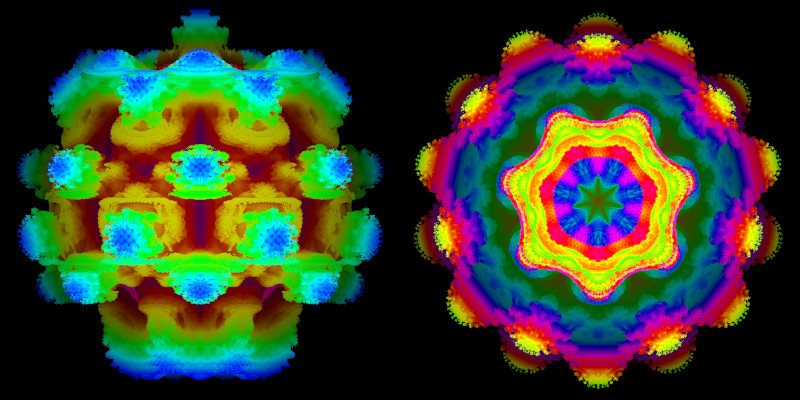
Wie aber bestimmt man die um x-, y- oder z-Achse gedrehten Startpunkte auf der Projektionsfläche? Beginnen wir
mit der Berechnung der Startpunkte. n ist hier die Nummer des Threads, aT deren Anzahl
und aufloesung die Anzahl der Pixel in einer Komponente.
startPunkte[n] = new ArrayList < float[]>();
for(int i=n*aufloesung/aT; i < (n+1)*aufloesung/aT; i++){
for(int j=0;j < aufloesung; j++){ float[] p = {-abstandScreen,-aufloesung/2+j,-aufloesung/2+i};
startPunkte[n].add(p);
}
}
}
Zu Beginn liegt die Projektionsfläche in einer y-z-Ebene im Abstand abstandScreen auf der negativen x-Achse. Schauen wir uns an, wie man die Startpunkte nun um die drei Achsen drehen kann:
bildPunkte[n] = new ArrayList < float[]>();raumBildPunkte[n] = new ArrayList < < float[]>();
float[] richtungEV ={-1,0,0}; //Richtungs-Einheitsvektor
alY = winkelY;alX = winkelX ;alZ = winkelZ;
raumENV[n] = drehenY(n,alY,richtungEV); //Raum-Einheits-Normalenvektor
raumENV[n] = drehenX(n,alX,raumENV[n]);
raumENV[n] = drehenZ(n,alZ,raumENV[n]);
for(int j=0;j < aufloesung*aufloesung/aT; j++){
float[] bP =drehenY(n,alY,startPunkte[n].get(j));bP = drehenX(n,alX,bP); bP = drehenZ(n,alZ,bP);
float[] raumBP = {bP[0]*fak,bP[1]*fak,bP[2]*fak};
bildPunkte[n].add(bP);raumBildPunkte[n].add(raumBP);
}
}
Ray-Tracing
Der Mesh-Tracing Ansatz liefert immerhin schon bessere Bilder als die Voxelmethode. Was aber noch nicht
zufriedenstellt, ist der Kontrast. Die Abstände von der Projektsionsfläche unterscheiden sich zu wenig.
Zudem sehen wir, aufgrund der parallelen Linien, den Gegenstand so, wie aus weiter Ferne.
Beide Probleme lassen sich mit dem Ray-Tracing-Verfahren umgehen. Die Idee können Sie durch die folgende
Animation nachvollziehen:
Wie beim Mesh-Tracing auch "stellen" wir eine Projektsionsfläche vor den Gegenstand. Die Linien aber gehen
nicht senkrecht von der Fläche zum Gegenstand, sondern kommen von einem "Auge", dass in einigem Abstand
hinter der Fläche liegt. Die Strahlen (ray) laufen vom Auge über die Fläche zum Gegenstand. Dies entspricht
dem natürlichen Sehvorgang. Mit Hilfe von Matrizen kann man dann, wie beim Mesh-Tracing, die Projektsionsfläche
an jede beliebige Stelle drehen. Auch der Abstand kann im Sketch variiert werden.
Die Verbesserung des Kontrast erreichen wir durch die Methode
distance estimation,
also Abstands-Schätzung. Lesen Sie sich die im Link angegebene Seite durch. Hier nur die Kurzform, inklusive
dazugehörige Programmcode:
Man läuft, im Gegensatz zum Mesh-Tracing, auf dem Strahl nicht in immer gleichlangen Schritten zum Gegenstand. Bei jedem
erfolgten Schritt, wird eine Abschätzung bezüglich der Entfernung zum Objekt vorgenommen. Anfangs sind
die Abstände dann recht groß und werden danach zunehmend kleiner. Dies sorgt für größere Geschwindigkeit
und ebenso für größeren Kontrast, denn nahe beieinander liegende Strahlen können ganz verschiedene
Abstand Abschätzungen bekommen. Und so kann man die Abstands-Schätzung realisieren:
int N = 0;
float dr = 1;
float nx = X;
float ny = Y;
float nz = Z;
float[] dE= new float[12];
float rad = sqrt(X*X+Y*Y+Z*Z);
while (N < maxIt) {
float powRad = pow(rad, exp);
float theta = atan2(sqrt(nx*nx+ny*ny), nz)*exp;
float phi = atan2(ny, nx)*exp;
nx = sin(theta)*cos(phi)*powRad+nx;
ny = sin(theta)*sin(phi)*powRad+ny;
nz = cos(theta)*powRad+nz;
dr = dr*exp*pow(rad, exp-1)+1;
rad = sqrt(nx*nx+ny*ny+nz*nz);
if (rad > 2) break;
N++;
}//end of while
dE[n] = 0.28*log(rad)*rad/dr;
return dE[n];
} //end of estimateDistance
n wird nur benötigt, wenn man mehrere Threads benutzt. Die übergebenen Werte X,Y und Z sind die
kartesischen Koordinaten zu zu überprüfenden Punktes. dr ist hier der näherungsweise Betrag der
Ableitung. dE[n] widerum ist die Abschätzung der Entfernung für jeden Thread. Eigentlich ist
der Faktor in der Literatur mit 0.5 angegeben. Weil hier aber immer wieder "overstepping" passiert
(man also über den gesuchten Punkt hinausgeht),hat sich der verwendete Faktor 0.28 bewährt.
Hier sind zwei Ergebnisse:
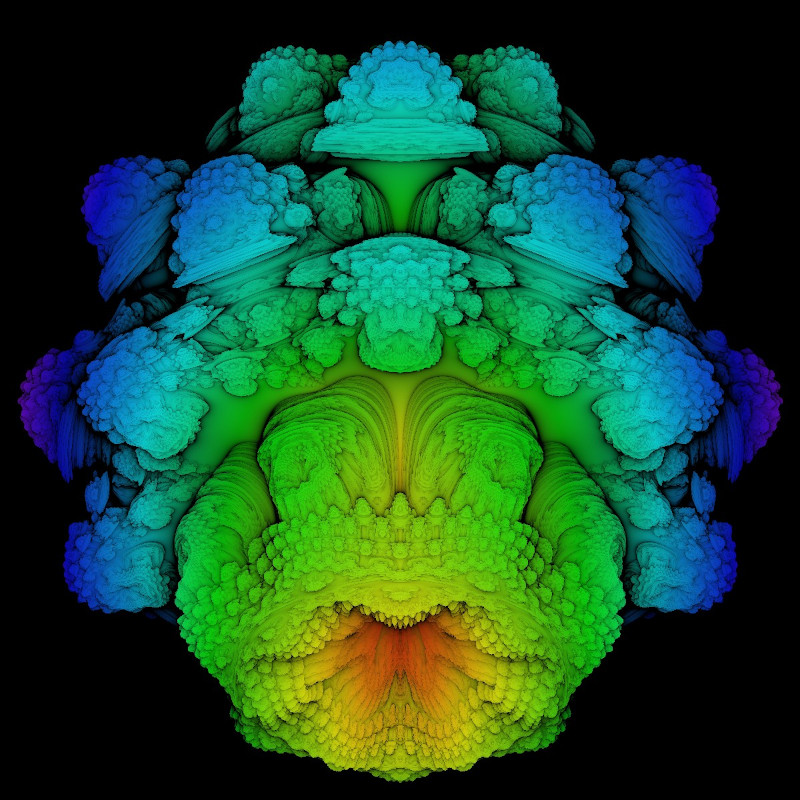
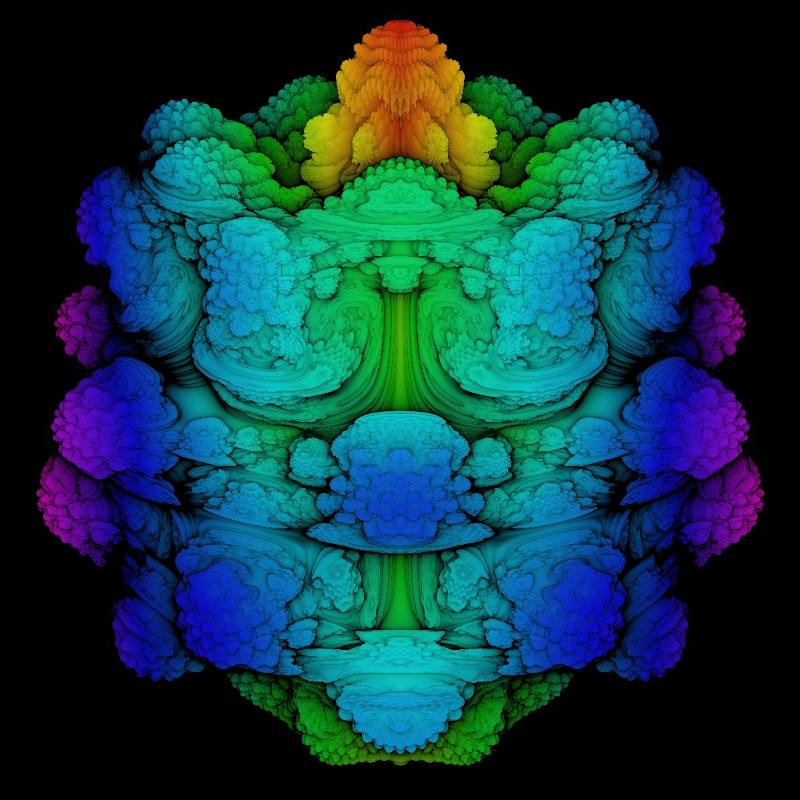
Unten kann der zugehörige Sketch runtergeladen werden. Beachten Sie, dass durch Tastatureingaben, neben
Drehungen um die drei Koordinatenachsen viele Parameter geändert werden können, wie zum Beispiel Farbe,
Helligkeit, Zoom etc. Einfach im Programmcode nachschauen!
Ähnlich wie im Kapitel Implizite Flächen drucken,
lassen sich auch Mandelbulb mit einem 3D-Drucker erzeugen:

Varianten des Mandelbulb
Es gibt unendlich viele Möglichkeiten, den Algorithmus mehr oder weniger zu verändern. Vergleichen Sie die folgende Zuordnungen für nx, ny und nz und vergleichen Sie mit weiter oben!ny = sin(theta)/(theta+1.1)*sin(phi)*powRad+ny;
nz = cos(theta)*powRad+nz;












Sketch Mandelbulb Voxel
sketch Mandelbulb Mesh-Tracing
sketch Mandelbulb Ray-Tracing
sketch Mandelbulb Ray-Tracing 2
Menu